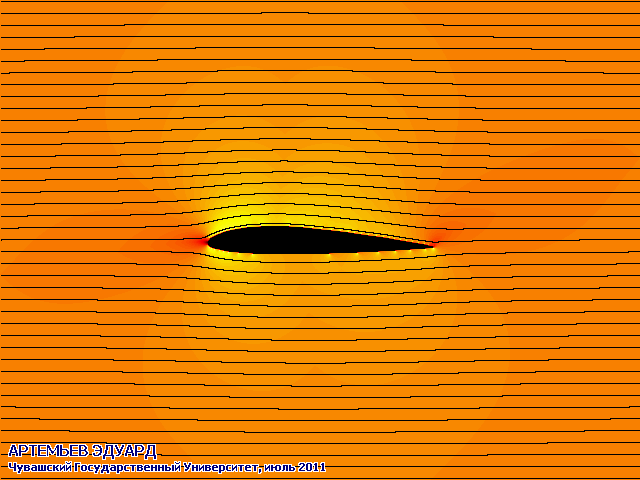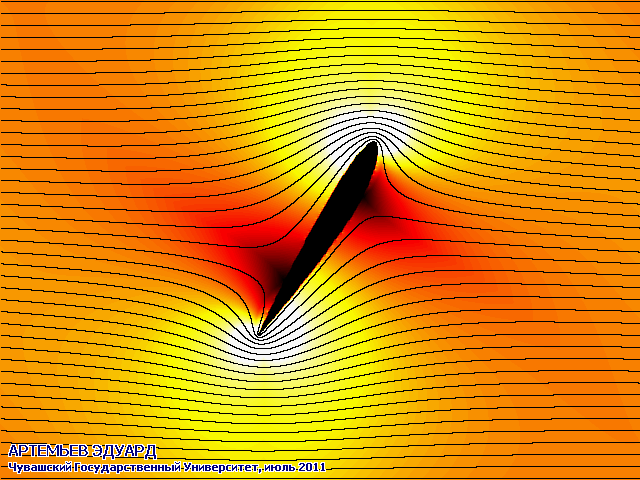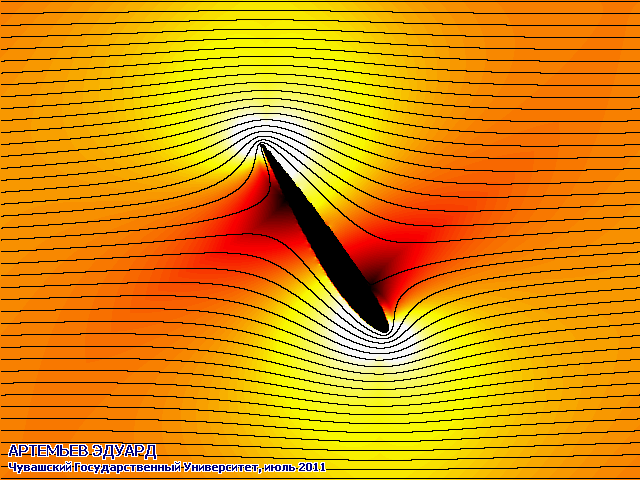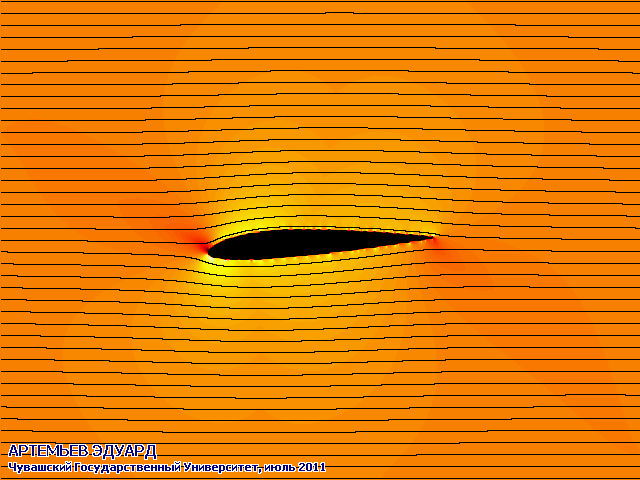
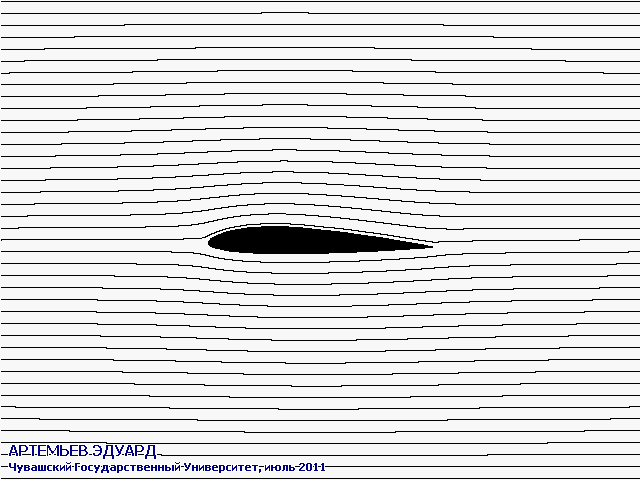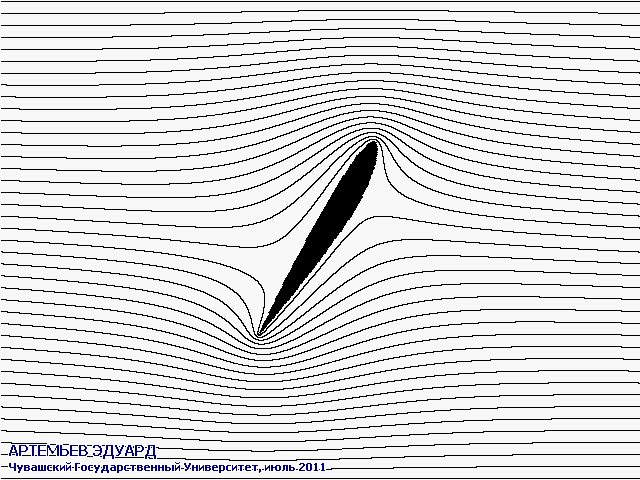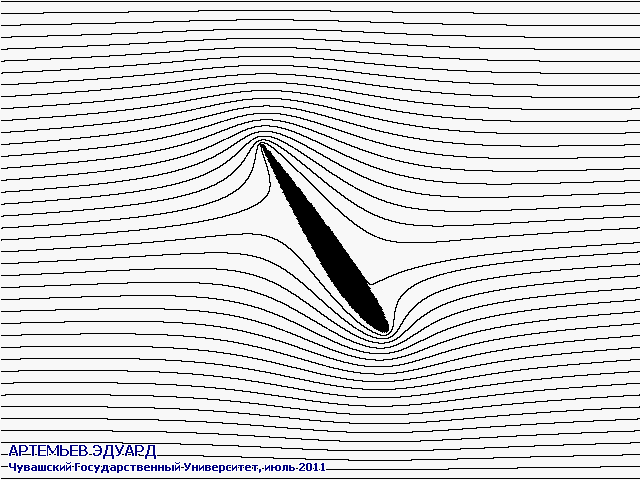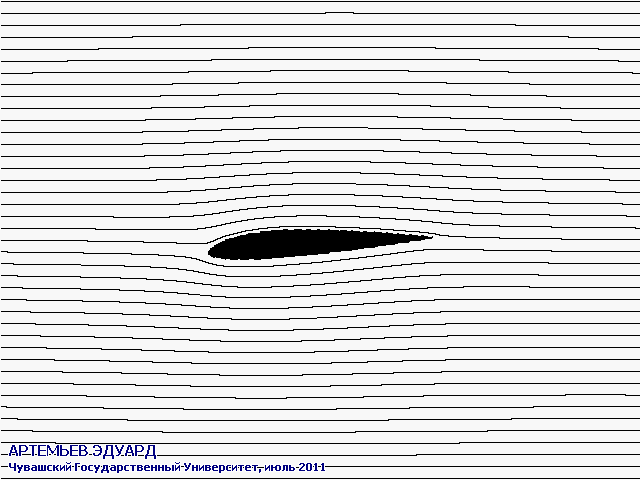
С помощью разработанного мною метода и созданной программы можно виртуально обдувать различные профили крыльев и другие детали под различными углами атаки.
На анимированных рисунках различными цветами обозначены скорости протекания воздуха или жидкости: чёрный - нулевая скорость, оттенки красного - более высокая скорость, оттенки жёлтого - ещё более высокая, белый - самая высокая скорость. Система отсчёта связана с крылом, поэтому оно считается неподвижным.
Поток из бесконечности набегает горизонтально слева.
Чёрными линиями на двух рисунках обозначены направления линий тока.
Программа предназначена для моделирования ламинарных (гладких) плоских течений, и никак не учитывает эффекта турбулентности (возникновения вихрей). Работой над турбулентными течениями планирую заняться через годик, сейчас времени не хватает.

федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Чувашский государственный университет имени И.Н.Ульянова» (ФГБОУ ВПО «ЧГУ им. И.Н.Ульянова») ФАКУЛЬТЕТ ИНФОРМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ КАФЕДРА МАТЕМАТИЧЕСКОГО И АППАРАТНОГО ОБЕСПЕЧЕНИЯ ИНФОРМАЦИОННЫХ СИСТЕМ ДИПЛОМНАЯ РАБОТА на тему: ОПТИМИЗАЦИЯ СХЕМЫ ПЕРЕВОЗОК НА ТЕРРИТОРИЯХ С НЕОДНОРОДНОЙ ПРОПУСКНОЙ СПОСОБНОСТЬЮ Дипломник студент группы ИВТ 31-06 Ёлкин Евгений Сергеевич Научный руководитель ст. преподаватель Артемьев Эдуард Иосифович. Заведующий кафедрой Д-р физ.-мат. наук, профессор Артемьев Иосиф Тимофеевич. Рецензент К. ф.-м. н., зав. кафедрой экономико-математического моделирования ЧГУ Никитин Виктор Васильевич. Чебоксары 2011 СОДЕРЖАНИЕ Введение 3 Глава 1. Постановка задачи поиска оптимальных маршрутов 4 Глава 2. Формализация задачи 6 Глава 3. Условие равновесия притоков-оттоков 8 Глава 4. Оптимизация плана перевозок 10 Глава 5. Кодирование входных данных в файле изображения 14 Заключение 17 Список использованной литературы 18 Приложение 1. Исходный код программы «Поиск оптимальных маршрутов» 21 Приложение 2. Результаты работы программы 34 ВВЕДЕНИЕ В настоящее время в России все больше и больше становятся востребованы компании оказывающие комплекс услуг по доставке грузов. Среди всего прочего, большое внимание уделяется логистике перевозок, которая включает в себя разработку схемы доставки, маршрутизацию движения транспорта, подбор вида одной или нескольких транспортных единиц, перегрузку из контейнеров, вагонов в авто транспорт или наоборот, разбивку груза в пути или доукомплектовку и так далее. В рамках данной работы рассматривается задача построения оптимальных схем доставки какого-либо продукта от поставщиков к потребителям. От классической транспортной задачи (задача Монжа–Канторовича), она отличается учётом особенностей местности, по которой будут осуществлены перевозки: наличие дорог, препятствий, пропускная способность отдельных участков. В работе рассмотрены методы программного решения оптимизации схемы перевозок. Полученные решения представляются в наглядном графическом виде и представляют собой схему оптимальных маршрутов, привязанных к конкретной карте местности. Представленная модель выходит далеко за рамки абстрактной задачи о доставке продукта из пункта «А» в пункт «Б». Рассмотренный метод планирования существенно повышает КПД перевозок, снижает бюджет на доставку грузов. С уважением Ёлкин Евгений. 05.05.2011. ГЛАВА 1 ПОСТАНОВКА ЗАДАЧИ ОБ ОПТИМАЛЬНЫХ СХЕМАХ ДОСТАВКИ Рассмотрим задачу построения оптимальных схем доставки какого-либо продукта от поставщиков к потребителям. Будем считать, что транспортировка продукта осуществляется на некоторой прямоугольной области. В одни точки области осуществляется приток продукта, из других точек осуществляется его отток (рис. 1.1). Точками притока можно обозначить склады продукции или производящие предприятия, а точками оттока – торговые центры, в которых товар попадает в руки конечного потребителя. Изначально известны координаты точек притока и оттока продукта. Также известны мощности поставщиков и потребителей, т.е. величины продукта, которые производятся (потребляются) за единицу времени. Считаем, что сумма мощностей производителей равна сумме мощностей потребителей, т.е. речь идёт о транспортной задаче закрытого типа. Также известны цены перевозки товара на различных участках рассматриваемой прямоугольной области. Под ценами на перевозку единицы товара на единицу расстояния можно понимать как финансовые затраты, так и затраты по времени. Вообще, если речь идёт о денежных затратах, то характеристикой места будет являться удельная стоимость перевозки, а если речь идёт о затратах времени – пропускная способность местности. Требуется составить оптимальный план перевозок на прямоугольной области, при котором общая стоимость перевозок будет минимальной. Забегая вперёд, скажем, что решение задачи предполагает правильное заполнение матрицы перевозок, которая будет рассмотрена в следующей главе, и графическое построение схемы маршрутов перевозок на карте местности. ГЛАВА 2 ФОРМАЛИЗАЦИЯ ЗАДАЧИ Для решения рассматриваемой задачи введём ряд обозначений и структур информации. Во-первых, разобьём рассматриваемую прямоугольную область на вокселей. Таким образом мы упростим модель до перемещения продукта между четырёхсвязными прямоугольными областями. Т.е. такими областями, каждая из которых имеет только 4 соседних элемента: верхний, нижний, правый, левый. Теперь пространство перемещений представляется прямоугольной матрицей, где продукт перемещается из одной ячейки в одну из черырёх соседних ячеек. Кстати, для хранения информации о характере таких перемещений, введём массив inp[x,y,i], где x,y – координаты вокселя, а i – номер направления притока (рис. 2.2). Отметим, что каждая ячейка имеет 5 направлений притока: один приток извне и четыре притока от соседних ячеек. Величина притока может принимать как положительные, так и отрицательные значения. Отрицательная величина притока может быть интерпретирована как отток продукта. Так же введём массив price[x,y] для хранения информации об удельных ценах перевозок внутри вокселей. Общую стоимость перевозок по территории вокселя будем вычислять как . (2.1) Заметим, что стоимость перевозок пропорциональна сумме квадратов притоков. Т.е. сумма квадратов притоков-оттоков рассматривается как показатель интенсивности товарооборота. Почему именно сумма квадратов, а не суммарный приток? Такой подход объясняется удобством использования суммы квадратов для нахождения экстремумов функции стоимости, что будет показано в последующих главах. К тому же сумма квадратов является инвариантной характеристикой товарооборота в ячейке, независимой от выбора направления координатных осей. ГЛАВА 3 УСЛОВИЕ РАВНОВЕСИЯ ПРИТОКОВ-ОТТОКОВ На основе обозначений введённых в предыдущей главе, запишем условие равновесия притоков-оттоков. Для одного вокселя оно принимает вид . (3.1) Т.е. равенство нулю суммы притоков ячейки является условием того, что в ней не возникнет переполнения или дефицита продукта. Иначе говоря, сумма притоков должна быть равна сумме оттоков. Соблюдение условия равновесия каждой отдельной ячейки матрицы гарантирует равновесие матрицы транспортировок вцелом. Аналогией закона равновесия является первый закон Кирхгофа (закон токов Кирхгофа), который гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком). Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины. Любое состояние матрицы, при котором соблюдается условие равновесия притоков, является одним из возможных решений транспортной задачи, но не обязательно оптимальным. Руководствуясь только условием равновесия притоков можно найти стартовый план перевозок продукта, после чего останется только привести его к оптимальному виду путём преобразований. Кстати, так и работает программа «Поиск оптимальных маршрутов», созданная автором: 1) нахождение неоптимального стартового решения, удовлетворяющего условию равновесия; 2) постепенная оптимизация найденного решения. Метод оптимизации плана перевозок по стоимости будет рассмотрен в следующей главе. ГЛАВА 4 ОПТИМИЗАЦИЯ ПЛАНА ПЕРЕВОЗОК Рассмотрим особенности оптимизации плана перевозок между четырьмя соседними ячейками матрицы транспортировок (рис. 4.1). Считаем, что для каждой из этих ячеек соблюдено условие равновесия притоков-оттоков. Попробуем внести изменение в характер их взаимодействия, не нарушая условия равновесия. На рисунке 4.2 показана возможная схема такого изменения. Все внутренние взаимные связи между ячейками мы изменим на величину Delta таким образом, чтоб суммарная стоимость перевозок минимизировалась. Другими словами, проведём минимизацию стоимости путём варьирования (изменения) величины Delta. Для этого воспользуемся математическим пакетом Maple. Листинг работы в системе Maple. Итак, с помощью системы Maple нашли оптимальное значение величины Delta для получения минимальной стоимости перевозок на территории четырёх соседних ячеек: (4.1) При таком изменении дельта решение оптимизируется для четырёх соседних ячеек. Многократно повторяя такую оптимизацию для различных малых групп матрицы транспортировок, мы добьёмся постепенной оптимизации матрицы вцелом. Отметим, что представленный метод был реализован в программе «Поиск оптимальных маршрутов» и показал себя надёжным, но медленным, требующим значительных затрат времени на проведение вычислений. ГЛАВА 5 КОДИРОВАНИЕ ВХОДНЫХ ДАННЫХ В ФАЙЛЕ ИЗОБРАЖЕНИЯ Программа «Поиск оптимальных маршрутов» в качестве входных данных берёт информацию из изображения-карты, подготовленной заранее в редакторе Paint. Предполагается, что каждое такое изображение содержит карту какой-то местности, характеристики которой закодированы с помощью RGB-составляющих цвета. В программе принят следующий способ кодирования: R (red) ? используется для указания мощностей поставщиков; G (green) ? используется для описания цены перевозки в данном месте; B (blue) ? используется для кодирования мощностей потребителей. Такой подход значительно облегчает процесс формирования входных данных, ведь для создания карт можно использовать популярные графические редакторы. Такая методика является хорошей заменой «старому доброму» составлению громоздких текстовых файлов с числовыми данными. Итак, для создания карт местности можно использовать те графические редакторы, которые позволяют точно регулировать цвета по модели RGB. Одним из таких редакторов является Microsoft Paint, позволяющий задавать цвета с помощью инструмента «Изменение палитры» (рис. 5.1). В качестве характеристики пропускной способности места была использована удельная стоимость перевозки Price. В программе она вычисляется по формуле Price= . Таким образом величина Price принимает целые значения в диапазоне от 1 до 35903328718. Значение G=1 соответствует самой высокой пропускной способности (низкой стоимости), значение G=256 ? самой низкой пропускной способности (высокой стоимости). Считается, что 256 различных значений Price вполне достаточно для описания различных дорожных и внедорожных условий перевозок. Таблица кодирования стоимости перевозки приведена на следующей странице. Программа, представленные в данной работе, распознаёт изображения, сохранённые в растровом формате BMP (Bitmap Picture). При сохранении карт лучше выбирать режим «BMP 24-разряда (бита)». Таблица кодирования стоимости перевозки Price с помощью градации зелёного цвета G. ЗАКЛЮЧЕНИЕ Результатом выполнения данной работы стало создание программы «Поиск оптимальных маршрутов». Программа выполнена в среде программирования Lazarus, являющейся свободным программным обеспечением. Этот факт сразу же отметает возможные сомнения в легальности использования программных средств для её создания. В данном труде разобран принцип работы программы. Рассмотрены примеры её использования. Программа, исходный код которой представлен в данной работе, может быть усовершенствована до более функциональной коммерческой версии, которая может быть использована менеджерами крупных компаний для организации оптимальной схемы перевозок грузов. Среди очевидных плюсов программы следует отметить наглядный графический интерфейс, а также возможность сохранения этапов поиска оптимального решения в виде упорядоченного набора изображений. Дипломная работа включает также примеры промежуточных расчётов с помощью математического пакета Maple. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Акчурин И.А., Веденов М.Ф., Сачков Ю.В. Методологические проблемы математического моделирования в естествознании. // Вопросы философии, 1966, №4. Акчурин И.А., Веденов М.Ф., Сачков Ю.В. Познавательная роль математического моделирования. М.: 1968. Андрющенко М.Н., Советов Б.Я., Яковлев А.С. и др. Философские основы моделирования сложных систем управления // Системный подход в технологических науках (Методологические основы): Сборник научных трудов – Л.: Изд. АН СССР, 1989, с.67-82 Артемьев И., Сейфуллина С.В. Теория вероятностей для гуманитариев: Практикум. – Чебоксары: ООО «Атолл», 2005. – 56 с. Артемьев И., Унжакова Е. Простая информатика для гуманитариев: Лабораторный практикум. – Чебоксары: «Новое время», 2006. – 80 с. Артемьев И.Т. Методы оптимизации для гуманитариев: Практикум. – Чебоксары: ООО «Атолл», 2005. – 28 с. Артемьев И.Т. Методы оптимизации и повышения эффективности технологических процессов: Практикум / Учебное пособие. – Чебоксары: «Новое время», 2007. –60 с. Артемьев И.Т. Практикум по математике для гуманитариев. – Чебоксары: ООО «Атолл», 2005. – 56 с. Артемьев И.Т. Простая информатика для гуманитариев: Лабораторный практикум. – Чебоксары: ООО «Атолл», 2005. – 68 с. Артемьев И.Т., Артемьев Э.И. Теоретическая механика для гуманитариев: Практикум. – Чебоксары: ООО «Атолл», 2006. – 48 с. Артемьев И.Т., Жачева Е.Н. Дмитриев Д.Д. Чувашская национальная вышивка и программирование для гуманитариев: – Чебоксары: ООО «Атолл», 2005. – 40 с. Артемьев И.Т., Замкова Т.В. Информатика для гуманитариев: Практикум на ПК / Учебное пособие. – Чебоксары: ЧИ МГОУ, 2006. – 74 с. Артемьев И.Т., Ильина Л.А, Ильин Д.В. Программирование на алгоритмических языках: Лабораторный практикум. - Чебоксары: Изд-во Чуваш. ун-та, 2005. -100 с. Артемьев И.Т., Ильина Л.А. Вычислительная практика на ЭВМ: Учебное пособие. - Чебоксары: Изд-во Чуваш. ун-та, 2001. -104 с. Артемьев И.Т., Ильина Л.А. Численные методы. - Чебоксары: Изд-во Чуваш. ун-та, 2002. -88 с. Артемьев И.Т., Кириллов В.К., Ермолаева О.Н. Основы математической лингвистики для филологов. - Чебоксары: Изд-во Чуваш. ун-та, 2002. - 84 с. Артемьев И.Т., Новикова С.В. Программирование на языке TURBO PASCAL: - Чебоксары: Изд-во Чуваш. ун-та, 2000. -160 с. Батороев К.Б. Кибернетика и метод аналогий - М.: Высшая школа, 1974. Бир С. Кибернетика и управление производством - М.: Наука, 1965 Бублик Н.Д., Секерин А.Б., Попенов С.В. Новейшие компьютерные технологии прогнозирования финансовых показателей и рисков. – Уфа: 1998. Васильев В.И., Ильясов Б.Г., Валеев С.В., Жернаков С.В. Интеллектуальные системы управления с использованием нейронных сетей. – Уфа, 1997. Вейль Г. Полвека математики – М.: 1969. Иванов В.Т. Математическое моделирование. Модели оптимального управления (Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988. Иванов В.Т. Математическое моделирование. Модели оптимизации (Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988. Клаус Г. Кибернетика и философия - М.: Наука, 1963. Кудряшев А.Ф. О математизации научного знания // Философские науки, 1975, №4, с.137 Лотов А.В. Введение в экономико-математическое моделирование М.: Наука, 1984. Петров А.А. Экономика. Модели. Вычислительный эксперимент. – М.: Наука, 1996. Салихов М.В. К вопросу об эвристической активности математики // Философские науки, 1975, №4Ю с.152-155. Самарский А.А. Гулин А.В. Численные методы - М.: Наука, 1989. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 1998. Форрестер Дж. Мировая динамика - М.: Наука, 1978. Фролов И.Т. Гносеологические проблемы моделирования - М.: Наука, 1961. Шеннон Р. Имитационное моделирование систем - искусство и наука - М.: Мир, 1978 ПРИЛОЖЕНИЕ 1. ИСХОДНЫЙ КОД ПРОГРАММЫ «ПОИСК ОПТИМАЛЬНЫХ МАРШРУТОВ» НА ЯЗЫКЕ LAZARUS